Question
How fast do I have to drive my car in order to jump off of the ground when driving over a humpback bridge?
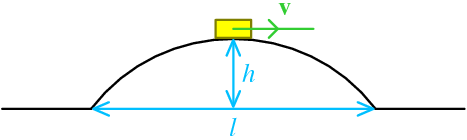
The bridge has a maximum height h from the level, and a (level horizontal) length l.
Answer
The velocity v required to leave the ground at the top of a humpback bridge:
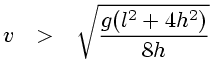
...where g is the acceleration due to gravity (about 9.81 m s-2 at sea level on Earth).
Derivation
The car will leave the ground at the top of the bridge if the gravitational force acting on it is insufficient to accelerate the car around the curvature of the bridge.
First, let's approximate the track of the bridge to an arc of a circle, whose radius (of curvature) is r. By working out what velocity is required to leave the ground at the exact top of the bridge, the maths is kept simple, as the gravitational force on the car is then acting directly along a radius of the circle. The situation looks like this:
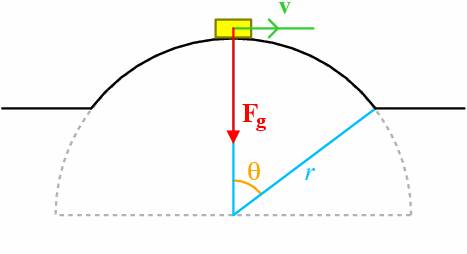
The gravitational force Fg acting on the car is Fg = m g, where m is the mass of the car. The force required to keep the car going around a circular path of radius r is Fc = m v2 / r, and therefore, for the gravitational force to be insufficient to supply this, we require:
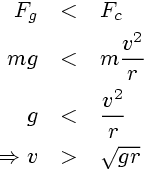
Clearly, it would be handier if we knew r in terms of the length l and height h of the bridge. The geometry looks like this:
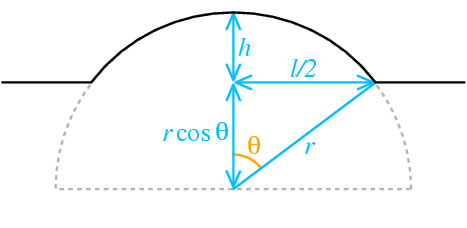
We notice that:
- From equating two radii of the circle, r cosθ + h = r.
- From Pythagoras on the right-angled triangle, r2 = (r cosθ)2 + (l / 2)2.
From (1) we get: r cosθ = r - h, which we can put into (2) to obtain: r2 = (r - h)2 + (l / 2)2. Solving for r, we find:
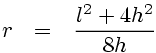
...so that our expression for the velocity then becomes:
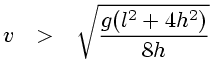
...which is our answer.