Question
At what radial distance must a satellite be placed in order to circle a planet in a geostationary orbit?
A geostationary orbit is an equatorial orbit with the same orbital period as the rotational period (day) of the planet, so that from the planet's surface, the satellite would appear to be fixed in the sky.
Answer
The radius r of a geostationary orbit around a planet of mass mp with rotational period Tp is:
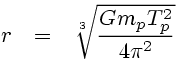
...where G is the Newtonian constant of gravitation, G = 6.6742(10)×10-11 m3 kg-1 s-2.
Example: the Earth
The mass of planet Earth, mp = 5.9737×1024 kg. The sidereal rotational period of Earth is about 23 hours, 56 minutes, and 4 seconds = 86,164 s. Now, a sidereal day is the time taken for the Earth to rotate once relative to the fixed background of stars, while the normal 24 hours is the time taken to rotate around once and be facing the Sun again, which is longer due to Earth's movement along its orbit. Putting these numbers into our formula, we get:
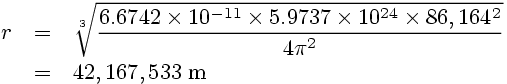
...or that the geostationary orbital radius about planet Earth is approximately 42,168 km.
Derivation
The problem looks like this:
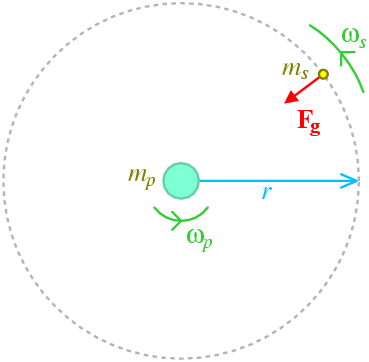
In order to keep a satellite of mass ms in a circular orbit of radius r with a constant orbital angular velocity of ωs, a centripetal force Fc needs to be supplied, where Fc = ms ωs2 r.
This will be provided by the force of gravitational attraction between the planet and the satellite, Fg = G mp ms / r2. So, we have:
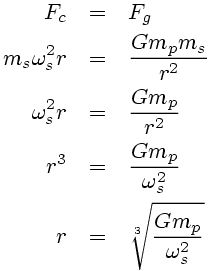
The angular velocity of the satellite ωs is related to its period of revolution Ts by ωs = 2 π / Ts. For a geostationary orbit, we would like this period to be equal to the (sidereal) rotational period of the planet, Tp. We can therefore substitute ωs = ωp = 2 π / Tp into the above equation to arrive at our final answer: