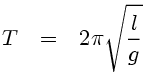Question
What is the time period of a simple pendulum?
Answer
The time period T taken for one oscillation (through small angles) of a simple pendulum of length l is:
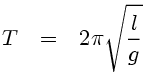
...where g is the acceleration due to gravity (about 9.81 m s-2 at sea level on Earth).
The frequency f of oscillations is of course the reciprocal of the time period, and is therefore:
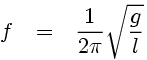
Derivation
The simple pendulum is a point mass m hanging vertically on the end of a string of constant length l whose other end is fixed. With a slight displacement of the pendulum from the vertical, the forces acting on the mass look like this:
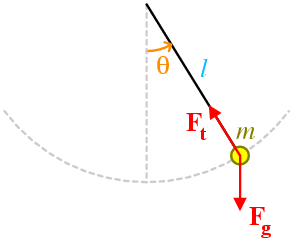
Fg is the force on the mass due to gravity, and Ft is the resulting force of tension in the string. The angle θ is measured between the string and the vertical.
Clearly, the mass will perform oscillations along an arc of a circle of radius l, so it's sensible to start by resolving forces along the radial and tangential directions of this circle. Ft already acts solely along a radius, but Fg can be resolved into radial and tangential components as follows:
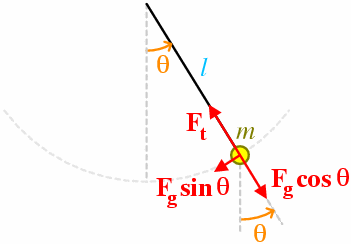
It's now clear that Fg sinθ is the restoring force that is pulling the mass along its circular path back towards its mean position (where the string is vertical and θ = 0). We can use the centre of the circle (the pivot-point of the pendulum) as a reference, and use Newton's second law in its angular form:
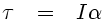
I.e. the torque τ is equal to the moment of inertia I multiplied by the angular acceleration α. The torque arising due to this restoring force acting at a distance l from the axis is τ = -l Fg sinθ, where the minus sign is required since the force is acting in the opposite direction to the sense of increasing θ. Now, the moment of inertia I about an axis for a point mass (of mass m) at a radial distance r is I = m r2 (by definition), and so I = m l2 in our case. Also, the gravitational force on the mass Fg = m g. Putting all this together, we have:
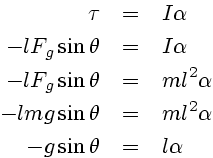
Now, the angular acceleration α is the time double-derivative of the angle θ. Putting this in, and re-arranging, we get:
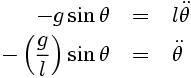
Unfortunately, this equation does not have a simple analytical solution. However, we can progress if we consider the pendulum as swinging through small angles only.
The small-angle approximation
For small values of the angle θ, the value of sinθ is approximately equal to the value of θ itself (provided that θ is measured in radians). This is apparent from the following diagram:
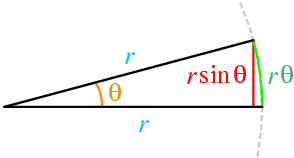
The length r sinθ is about the same as the length of the arc, r θ. So, r sinθ ≈ r θ, hence sinθ ≈ θ.
Using this approximation in our previous equation, we obtain:
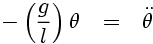
Now, this equation has the same form as the equation describing simple harmonic motion (SHM):

Where in our case, ω2 = ( g / l ) and the variable x is θ. So we have shown that, for small-angle oscillations, the movement of the pendulum is approximately simple harmonic, hence we can use the results from SHM. The frequency f of oscillations is related to ω by f = 2 π / ω. In our case, ω = √( g / l ), hence we have:
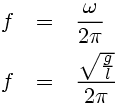
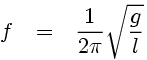
The time period T taken for one oscillation is simply the reciprocal of the frequency, T = 1 / f, and so we arrive at our final answer: