|
| Navigation<> |
One of these systems is a quantum well, fabricated by sandwiching a layer of semiconductor between two layers of another material with a higher bandgap. The motion of electrons and holes is frozen in the growth direction, and in modelling the system we may consider the electrons and holes as being essentially confined to a plane. As in bulk semiconductors, the Coulomb interaction between electrons and holes leads to bound states, known as excitons, which are extremely important for the optical properties of the quantum well.
The introduction of a strong magnetic field in the growth direction leads to further interesting phenomena in two-dimensional systems. At sufficiently low temperatures, many-electron correlations become important and new states of matter are formed. One of these states of matter is an incompressible quantum liquid, whose excitations carry fractional charge and obey fractional statistics. Spectroscopic techniques can be used to probe the properties of such systems, and excitonic effects are again of the utmost importance.
Our research was focused on a number of diverse problems in mathematical physics related to the theory of excitons in semiconductor nanostructures. Firstly, in an attempt to reach a full understanding of the well-known degeneracy of energy states for a two-dimensional exciton (hydrogen atom) we formulated the problem in momentum space. Projecting this two-dimensional momentum space onto the surface of a three-dimensional sphere not only explained the observed degeneracy, but also yielded a new integral relation in terms of special functions that had not previously been tabulated [28,30,31].
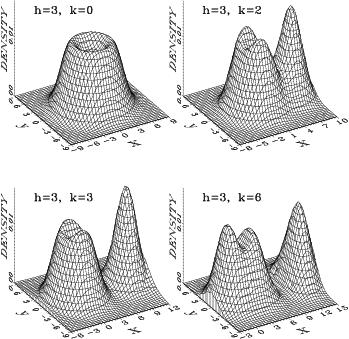
The second part of our research focused on an exciton against the background of an incompressible quantum liquid, which can be formed at certain ' filling factors when a two-dimensional electron gas is subjected to a strong perpendicular magnetic field at very low temperatures. Excitations of this quantum liquid with fractional charge and fractional statistics are known as anyons. An anyon exciton consisting of a valence hole and several anyons may be created as long as the hole is sufficiently far away from the electron layer to avoid destroying the quantum liquid. We have recently generalised the model of an anyon exciton [9-14] to consider an exciton consisting of a hole and an arbitrary number of anyons [33,34,37]. We have derived a full set of anyon exciton basis functions and classified these functions using a result from the theory of partitions. We also obtained several exact results, including the binding energy of a few-particle exciton with zero in-plane momentum and zero angular momentum. The Figure shows the electron density distribution in a four-particle anyon exciton [14] for different values of the exciton in-plane momentum and with electron-hole plane separation, h, equal to three magnetic lengths.
The work on this set of problems has resulted in several high-level
publications and conference presentations. David Parfitt, who
worked with Dr Portnoi on these problems, finished his PhD within
eighteen months, and his dissertation formed the basis of an invited
chapter in a recently published book on mathematical physics
[38].